Modelling Fantasy Football Points Scored 19-20 Season

Introduction to Fantasy Football

The English Premier League Fantasy Football is a game played alongside the English Premier League (EPL) that allows fans to create a team of Premier League footballers, under a number of constraints, and compete against other people’s teams. As EPL matches are played footballers are awarded points based on their individual and club performance, this in turn impacts their transfer value within the game. Each player builds a team with 100 million pounds so that anyone cannot just buy the 11 best footballers in the EPL, in addition no more than three players from the same club can be on the team. Each player’s aim is to create the best possible team within the budget and the three players from a club rule. Each week every player can make one transfer for free, selling one footballer and buying another to replace them staying within budget, and can make additional transfers at the cost of two points.

Players make transfers using statistics from the Fantasy Football website, personal evaluations of a footballer’s current form and educated guesses of future match results. In this notebook we use statistical models to attempt to find the best possible transfer each week by predicting the points every player will accrue in the next gameweek matches. In the EPL Fantasy Football players select not just a starting 11 but also 4 substitutes, in this work we ignore substitutions and concentrate on the starting team only.

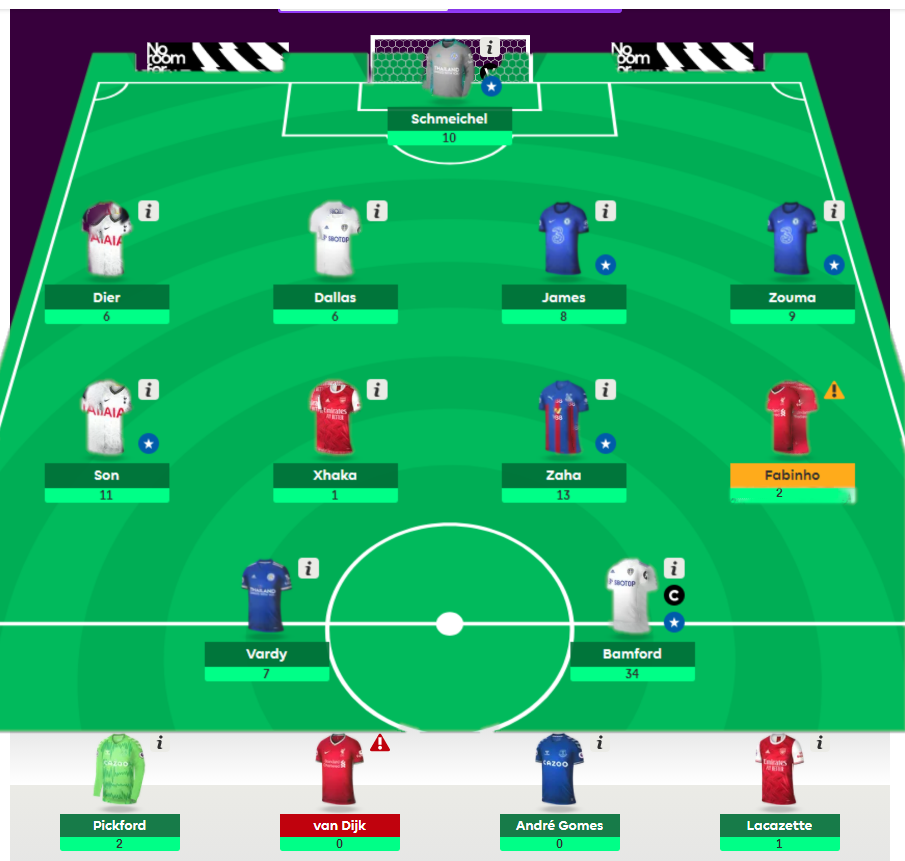
In Figure 1 an example fantasy football team is shown. The table shows the data at the end of the first three rounds for just three players, Harry Kane, Jonny Evans and Mo Salah.

The available data each week consists of statistics for individual player performance e.g. goals, assists, minutes played, transfer value, and fantasy football statistics e.g. fantasy points, ‘creativity’, ‘influence’ etc. In addition, we also have the match results themselves and future fixture information.

Figure 2 previews a selection of columns for a handful of players in the match data.

Like most events in 2020 the EPL was affected by Covid-19 and many matches were postponed. After a few months break the EPL returned without crowds and whilst there are many interesting questions posed by such an extended mid-season break and the absence of crowds, in this analysis we ignore any matches played after covid-19 impacted the EPL. Covid-19 first caused games to be postponed in Gameweek 28, therefore we model matches up to Gameweek 26 and the final week of predictions is Gameweek 27. In addition to Covid-19, Liverpool’s participation in the Club World Cup resulted in their match against West Ham United being postponed from Gameweek 18 to Gameweek 24 - we use the postponed fixture only for modelling team strength and do not count that game towards fantasy football points.

Exploration of the Data

The data used in this work is taken from the github page: https://github.com/vaastav/Fantasy-Premier-League/tree/master/data/2019-20 .

The first interesting question one must answer in EPL Fantasy Football is which formation to play, this leads to attempting to find the best value position. From the data, the most efficient position (in the sense of points per pound spent) is goalkeeper and the least efficient is midfield. This does not mean we shouldn’t favour midfielders because as long as the team is within the budget, the cost per point is not the most important factor. In the modelling stage we will allow any transfers that give valid formations.

Figure 3: The cost per point scored for each player aggregated within each club and position.

Looking at Figure 3 we can see that there is considerable variance between clubs, however we see that some clubs tend to have undervalued players and some have overvalued players. This is likely a consequence of under/over-rating certain teams and of popular footballers.

In Figure 4 we look at the average cost per point of individual footballers and highlight the best-performing players in each position. It is interesting to note that there appears to be footballers that are very cost-effective in a points per pound perspective and also footballers that seem to be greatly overvalued compared to the points scored. For example, if we look along the y-axis at 125 points scored there is a large variation of prices for midfielders and forwards.

In Figure 5 the Spearman correlation plot shows the correlation between the match statistic data and the weekly points (‘total points’), this gives an idea of the features we may want to include in the model to predict the weekly points for each footballer in the EPL. Note that although real-world match performance is important footballers are awarded fantasy football points based on a set of rules, and don’t necessarily reflect the best footballers. As we would expect, total points is most strongly positively correlated with clean sheets and goals scored and negatively correlated with goals conceded, suggesting that goals are an important indicator of points.

Modelling Player Performance in Fantasy Football

As stated in the introduction the aim of this work is to find the best transfer each week given the current starting 11, the available transfer budget and the upcoming fixtures. To do this the modelling problem can be stated as predicting the number of points every footballer in the league is expected to get in each gameweek. The approach used here is a two-step process: first, we model the strength of both teams in a match and then, we model the number of points each player in the match will score. To model the relative strengths of teams in a match-up we use a Bayesian hierarchical Poisson model that assigns an attacking and defensive strength factor estimated using previous results. The weekly points prediction for each footballer uses a random forest model that includes the team and opposition coeficients output from the first step.

The algorithm starts modelling data at game week 5, i.e. every team has five completed fixtures at this stage, and then gameweek 6 is the first week the model predicts fantasy football points. The algorithm is outlined below:

---

Algorithm: Predicting Footballer Fantasy Football Match Points

---

1. For loop over gameweek (gw) 5 to 26: each step 2-5 is run in every loop
2. Bayesian Poisson model is fit to the results up to and including gameweek gw; outputs the attack and defensive coefficients for each team.
3. Fit a random forest to the player performance statistics up to gameweek gw where weekly points is the dependent variable, and predict the points for each player in (gw + 1).
4. Use the predicted fantasy football points to find the best transfer (within budget and player-per-team constraints).
5. Return to step 1 unless gw = 26

---

There are a number of complications that are not mentioned above, e.g. creating variables for the random forest, and no Liverpool or West Ham United players in game week 18.

Modelling Team Attack and Defense Coefficient: Bayesian Poisson Model in JAGS

To model the score of a fixture, we model the expected number of goals each team scores using the Poisson distribution. The parameter in the Poisson distribution for the number of goals a team scores takes into account if a team was home or away, the attacking coefficient of that team, and the defensive coefficient of the opposition. The parameters in the model are estimated using all completed fixtures. The model for the expected number of goals scored by Team A against Team B is given by:

\[\\begin{align} Y & = \\text{Po} \\left( \\lambda \\right) , \\text{ where} \\\\ \\log \\left( \\lambda \\right) & = X\_h \\mathbb{1}\_h + \\alpha\_A + \\beta\_B . \\end{align}\]

The parameter λ is the expected number of goals scored by team A against team B, X_h is a random variable that adjusts the expected number of goals a team scores in a home game compared to an away game (it is well-known in football that home advantage confers a significant increase in the expected number of goals a team scores), 𝟙_h is the indicator of whether a team is home or away, α_A is the attacking coefficient of team A and β_B is the defensive coefficient of team B.

The parameters in the model have the following prior distributions: \(\\begin{align} X\_h & \\sim \\mathcal{N} \\left( 0, 0.0001 \\right) \\\\ \\alpha\_A & \\sim \\mathcal{N} \\left( \\mu\_{\\alpha\_A} , \\tau\_{\\alpha\_A} \\right) \\\\ \\beta\_B & \\sim \\mathcal{N} \\left( \\mu\_{\\beta\_B} , \\tau\_{\\beta\_B} \\right) . \\end{align}\)

The hyper-parameters of the attacking and defensive coefficients have the following prior distributions: \(\\begin{align} \\mu\_{\\alpha\_A} & \\sim \\mathcal{N} \\left( 0, 0.0001 \\right) \\\\ \\mu\_{\\beta\_A} & \\sim \\mathcal{N} \\left( 0, 0.0001 \\right) \\\\ \\tau\_{\\alpha\_A} & \\sim \\Gamma \\left( 0.01, 0.001 \\right) \\\\ \\tau\_{\\beta\_A} & \\sim \\Gamma \\left( 0.01, 0.001 \\right) . \\end{align}\)

The normal distributions in all of the above are parameterised by the mean and the precision; this is same parameterisation used by the JAGS package.

To fit the Bayesian Poisson model described above we use Just Another Gibbs Sampling (JAGS); the R package rjags is used to connect to the JAGS library from within R. JAGS uses the BUGS (Bayesian Gibbs Sampling) language; first, create a bugs model file and then in R use rjags to run the MCMC algorithm with user-defined parameters, burn-in periods, number of chains etc.

The Bayesian Poisson model is fit at gameweek 26 to the full fixtures played up to and including that week. In Table 1 the attacking and defensive coefficients and the home advantage s given for Liverpool at home to West Ham United. This can be used to calculate the expected number of goals that each team scores against the other.

Team	Attacking Coefficient	Defensive Coefficient	Home Advantage
Liverpool	0.493	-0.39	0.032
West Ham United	-0.096	0.157	0

Although we only want the attacking and defensive coefficients to model the predicted fantasy football points for each player, we can use the Poisson model to calculate the expected number of goals in the fixture Liverpool vs. West Ham United. Substituting the estimated coefficients into the model we find the expected number of goals for both teams to be Liverpool = 1.97 and West Ham United = 0.61.

Predicting Player Fantasy Football Points: Random Forest

The random forest model is the piece that actually predicts the number of points we expect each footballer in a premier league fixture to score. Random forest models work by fitting a large number of deep decision trees and then averaging the individual trees. The process involves at each tree randomly subsampling the observations (rows of the data) to fit and at each node within each tree randomly subsampling the features to split on (columns of the data). This tends to achieve good results compared to other classification or regression techniques.

There are two established methods (that are frequently encountered) for assessing variable importance, Gini node impurity and random permutation mean-square error. It is suggested that Gini importance can inflate the importance of continuous variables or discrete variables with a large number of categories. Generally, we prefer to use the random permutation MSE which uses out-of-bag sampling to calculate these values. Here, we find that both metric find very similar variable importance results.

Gini node impurity measure considers the decrease in Gini impurity at each split in each tree. The Gini impurity is calculated as the improvement we see at a node due to splitting on a variable compared to before the split.

The random permutation MSE variable importance is calculated by randomly permuting the values in that variable in the out-of-bag sample and comparing the MSE to the original data (without random permutation of the values). The idea is that if a variable is important then if we randomly permute the values in that variable we should find a decrease in predictive accuracy.

The variable plots in this case agree with each other to a large extent. The most important variables are form and value, which is to be expected, and the next most important are the attacking and defensive coefficients of both teams.

Evaluating Model Performance: Recent Form Model vs. Jags-Random Forest

To evaluate the performance of the proposed model we compare the points predictions against a “Naive Recent Form” model; the points prediction for a footballer in the next game is the average of the points in the previous five matches. The model is considered naive in this setting because it does not take into account the opponent in either the previous matches or the upcoming fixture.

The sum of squares error is used to calculate the error between the model prediction and the observed points accrued by the player. We also show the performance of each method in selecting the best transfer each week based on predicted points given the budget and team constraints.

The weekly predicted points scored and actual points scored is illustrated in the plot below for a selection of players.

In Figure 6 we can see that the predicted points match up very well with the actual points scored by both players, more so in the case of the random forest-jags approach but it’s only two players, except when the player scores very highly. This pattern is seen in the plots of many players.

Each gameweek the two models predict the points scored by each player in the upcoming fixtures, the residual sum of squares between the predicted points scored and the actual points scored for both methods is calculated.

In Figure 7 We see that consistently the random forest-JAGS method outperforms the naive recent form model using this measure. In fact, in every game week that we predict the fantasy football points the random forest-JAGS model has a lower sum of squares error to the actual points scored.

The weekly points scored and cumulative points scored given in Figure 8 assume a starting team of Tim Krul (GK), Virgil van Dijk, César Azpilicueta, Jonny Evans (DEF), Mohamed Salah, Kevin De Bruyne, Marc Albrighton, Andros Townsend, Ayoze Pérez (MID), Jordan Ayew and Christian Benteke (FWD) and an assumed bench cost of the remaining transfer budget at the start of week 1. Each week the models predicts the expected points scored by each player and the optimal transfer is made (allowing valid changes of formations and obeying the 3 players per club rule) within budget. The results will have a lot of variation and should not be taken as validation of either method, the results shown in Figure 7 are more significant.

Possible Future Directions

In this work we partially answered the question of which one transfer should we make each week given budget constraints. However, there is a lot more that could be added to the models to create more accurate predictions of the points each footballer will get each week for a given fixture. For example

• Use information from the player news: contains injury information, loan status etc.
• Collect weather data near the home stadium
• Other competition information, e.g. played in international fixture/European club fixture (particularly if playing away)